Nottingham FP Lab Blog

Collecting isos on regular types

by Thorsten on July 15, 2005.
Tagged as: Lunches.

After Conor’s report from the Scottish Programming Language Workshop, I was talking about my new hobby of collecting isomorphisms on regular types (0,1,+,x,List) and claimed that

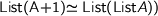
$\mathrm{List}(A+1)\simeq \mathrm{List}(\mathrm{List} A))$

\mathrm{List}(A+1)\simeq \mathrm{List}(\mathrm{List} A))

would be such a beast. Conor discovered that this was wrong and the corrected iso is

$\mathrm{List}(A+1)\simeq \mathrm{List}(\mathrm{List} A))\times \mathrm{List}(A)$

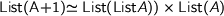
\mathrm{List}(A+1)\simeq \mathrm{List}(\mathrm{List} A))\times \mathrm{List}(A)

which is indeed an instance of the other beast in my rather modest collection :

$\mathrm{List}(A+B) \simeq \mathrm{List}(\mathrm{List}(A)\times B)\times\mathrm{List}(A)$ .

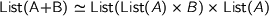Graham asked about the connection to numbers and Conor was happy to oblige by noting that arithmetically

$\mathrm{List}(A) = {1\over{1-a}}$

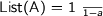
\mathrm{List}(A) = {1\over{1-a}}

and checking that the general iso is justified by this interpretation.
Since I got bored this afternoon, waiting for a phone call, I hacked in the first iso into Haskell (can I use lhs here? [you can now - Ed])

$%format phi = “\phi” %format phii = “\phi^\prime” \begin{code} phi :: [Maybe a] -> ([[a]],[a]) phi [] = ([],[]) phi (an:ans) = case an of Nothing -> (as:aas,[]) Just a -> (aas,a:as) where (aas,as) = phi ans \end{code} \begin{code} phii :: ([[a]],[a]) -> [Maybe a] phii ([],[]) = [] phii (as:aas,[]) = Nothing:(phii (aas,as)) phii (aas,a:as) = (Just a):(phii (aas,as)) \end{code}$

%format phi = “\phi” %format phii = “\phi^\prime” \begin{code} phi :: [Maybe a] -> ([[a]],[a]) phi [] = ([],[]) phi (an:ans) = case an of Nothing -> (as:aas,[]) Just a -> (aas,a:as) where (aas,as) = phi ans \end{code} \begin{code} phii :: ([[a]],[a]) -> [Maybe a] phii ([],[]) = [] phii (as:aas,[]) = Nothing:(phii (aas,as)) phii (aas,a:as) = (Just a):(phii (aas,as)) \end{code}