Nottingham FP Lab Blog

From High-school algebra to University algebra

by Thorsten on November 25, 2005.
Tagged as: Lunches.

An equation like $a \times (a+1) = a^2 \times a$ can be read as an equation over the natural numbers or as an isomorphism which hold in a category with the appropriate structure. The problem of solving equations over 1,+,x,^ in the natural numbers is called the High School Algebra problem and Tarski asked whether the equations we learn at school are complete. Roberto di Cosmo and others observed that this is closely related to isomorphisms in cartesian closed categories with + (I recommend Roberto’s very readable survey).

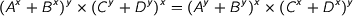Wilkie showed that high school algebra is incomplete, the core of his counterexample is that we cannot show using the equations of High School Algebra that $A\times D = B\times C$ implies $(A^x + B^x)^y\times (C^y+D^y)^x = (A^y+B^y)^x\times (C^x+D^x)^y$ . I observed that this isomorphism is derivable using dependent types and exploiting 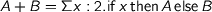$A+B = \Sigma x:2.\mathrm{if}\,x\,\mathrm{then}\,A\,\mathrm{else}\,B$ and $A\to\Sigma x:B.C\,x = \Sigma f:A\to B.\Pi x:A.C\,(f\,x)$ . This observation leads to formulating what I call university algebra which generalizes high school algebra by using $$\Sigma$ and $$\Pi$ .

Here are some laws of university algebra:

$\Pi a:A.\Sigma b:B\,a.C\,a\,b = \Sigma f:(\Pi a:A.B\,a).\Pi a:A.C\,a\,(f\,a)$
$\Pi p:(\Sigma a:A.B\,a).C\,p = \Pi a:A.\Pi b:B\,a.C (a,b)$
$\Sigma a:A.\Sigma b:B\,a.C(a,b) = \Sigma p:(\Sigma a:A.B\,a).C\,p$
$1\to A = A$
$1\times A = A$
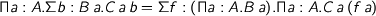
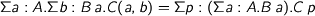
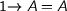
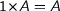
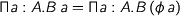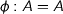$\Pi a:A.B\,a = \Pi a:A.B\,(\phi\,a)$ where $\phi:A = A$ is an isomorphism
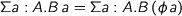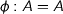$\Sigma a:A.B\,a = \Sigma a:A.B\,(\phi\,a)$ where $\phi:A = A$ is an isomorphism

When deriving isomorphisms we may use equalities of types which relies on equality of terms. We can read those as equations on natural numbers, every type corresponds to a number and
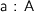a : A can be read as 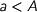$a < A$ . I believe that unlike High School algebra, University Algebra is complete. Without 0 it may even be decidable, with 0 it isn’t because we can encode consistency of formulas of intuitionistic predicate logic in it.