Nottingham FP Lab Blog

monads and comonads

by Thorsten on December 16, 2005.
Tagged as: Lunches.

Inspired by the discussion on comonads we had two weeks ago I gave a little tutorial on monads and comonads which was finished off by Neil.

A standard example for monads are arising from substitution: Consider a the set of terms 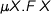$\mu X.F\,X$ given by an endofunctor 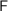. Terms over a given set of variables can be encoded as $M_F\,X = \mu X.X + F\,X$ and this gives rise to a monad, where $\eta \in X \to M_F\,X$ embedding variables into terms and $\hat{f}\in M_F\,X\to M_F\,Y$ corresponds to applying a substitution given by $f\in X\to M_F\,Y$ .

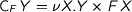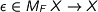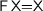Dually, we construct a comonad $C_F\,Y = \nu X.Y\times F\,X$ which corresponds to infinite terms with labels, the counit $\epsilon \in M_F\,X \to X$ returns the top-level label and $\check{f}\in C_F\,X \to C_F\,Y$ relabels a tree according to a relabelling function $f \in X \to C_F\,Y$ . The example of streams which inspired this little tutorial is an instance of this, if we choose $F\,X=X$ , i.e. the identity functor, since $C_F\,Y = \nu X.Y\times X \simeq \mathbb{N}\to Y$ .

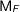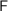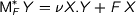Neil explained that the monad M_F is the free monad over , i.e. this is given by applying the left adjoint of the forgetful functor from the category of monads to the category of endofunctors, dually C_F is the cofree comonad. Neil and his student Fed also investigated the monad $M^*_F\,Y=\nu X.Y + F\,X$ which is the fully iterative monad over 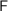. However, it seems that its dual 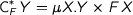$C^*_F\,Y=\mu X.Y\times F\,X$ has not yet attracted much attention.