Nottingham FP Lab Blog

Iterative and Completely Iterative Monads

by Mauro Jaskelioff on February 3, 2006.
Tagged as: Lunches.

Neil said:

Today I spoke about iterative and completely iterative monads. These
monads constitute terms which are the solutions of equations of the
form
$f\colon E \rightarrow X + FE$

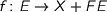
for some functor $F$ . The monad $TA = \nu X.A+FX$ is the smallest monad which contains unique solutions for all such equations. The rational monad
is the smallest monad which contains solutions of such equations where 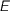$E$ is finite.

An open question is to understand the monad of solutions to equations defining not just terms but operators such as

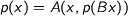
$$p(x) = A(x,p(Bx))$$

We call these algebraic terms. Getting freeness properties for such
classes of terms is the key to using the coproduct of monads to
combining such iterative theories

For references see the work of Milius and some of my own.

Stefan Milius, Completely iterative algebras and completely iterative
monads, Information and Computation, v.196 n.1, p.1-41, January 10,
2005. An old preprint.

Ghani, N and Lüth, C and de Marchi, Solving Algebraic Equations using Coalgebra, Journal of Theoretical Informatics and Applications, 2003.

Neil Ghani and Tarmo Uustalu, Coproducts of Ideal Monads, Journal of Theoretical Informatics and Applications, 2004.