Nottingham FP Lab Blog

Parsing with distinction

by Wouter on February 13, 2006.
Tagged as: Lunches.

Thorsten and I have been working on distinguishing non-isomorphic types. Along the way, we encountered some interesting connections with monadic parser combinators.

Traditionally, monadic parser combinator have a type:

Given a sequence of input symbols, the parser returns a finite powerset of possible leftovers. These parsers don’t return the information parsed, but merely recognize whether a given string is in the language.

Such parser combinators can actually be run:

$\mbox{run} \, : \, PC \, i \to i^* \to \mathrm{Bool}$

by simply checking whether all the input has been consumed, i.e. the empty string is in the resulting powerset.

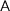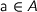Context-free types over an index set consist of a 0,1 and a parameter $a \in A$ . Furthermore, context-free types are closed under products, coproducts and least fixed points. We consider such types isomorphic if their well-known functorial semantics are naturally isomorphic. They clearly resemble context-free grammars. Interestingly, the same monadic parser combinators can be used to distinguish non-isomorphic types.

Instead of parsing input strings, we have to be a bit more careful. As the product commutes and the coproduct is not idempotent, we move from sequences to multisets. We represent a multiset as follows:

$\mathsf{type}\, MS \, i = [(i,\mbox{Nat})]$

Such multisets form a monad, a fortiori, they are an instance of MonadPlus. The old-school monadic parser combinators also work for multisets. We get parser combinators of the following type:

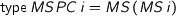
$\mathsf{type}\, MSPC \, i = MS \, (MS \, i)$

Using these parser combinators we can now count the number of inhabitants of a given type. As two non-isomorphic types will have a different number of inhabitants for some input, we have a structured manner to search for disparities.

If you’re particularly interested have a peek at the implementation and the paper Thorsten and I are working on.