Nottingham FP Lab Blog

Uniqueness Logic

by Wouter on March 24, 2006.
Tagged as: Lunches.

I talked about the firsty twenty odd pages of Dana Harrington’s thesis, which Hank had kindly pointed out to me. Uniqueness logic is used by Clean to write fast functional programs and model safe IO. The core idea is to keep track of which values are unique, i.e. can be represented by a single cell of memory that is never copied or thrown away. To accomplish this, uniqueness logic distinguishes between unique and non-unique values in their type. A type 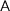A is considered unique; it’s non-unique counterpart is denoted by A^\ast.

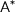The following sequents describe the most important rules (excuse the crummy latex):

$\frac{}{A \vdash A}$ $\frac{\Gamma \vdash A}{\Gamma \vdash A^{\ast}}$ $\frac{\Gamma, A \vdash B^\ast}{\Gamma, A^\ast \vdash B^{\ast}}$ $\frac{\Gamma \vdash A \quad \Delta \vdash B}{\Gamma, \Delta \vdash A \otimes B}$ $\frac{\Gamma, A, B \vdash C}{\Gamma, A \otimes B \vdash C}$ $\frac{\Gamma \vdash A \quad \Delta, B \vdash C}{\Gamma, \Delta, A \multimap B \vdash C}$ $\frac{\Gamma, A \vdash B}{\Gamma \vdash A \multimap B}$

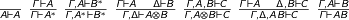
$\frac{}{A \vdash A}$ $\frac{\Gamma \vdash A}{\Gamma \vdash A^{\ast}}$ $\frac{\Gamma, A \vdash B^\ast}{\Gamma, A^\ast \vdash B^{\ast}}$ $\frac{\Gamma \vdash A \quad \Delta \vdash B}{\Gamma, \Delta \vdash A \otimes B}$ $\frac{\Gamma, A, B \vdash C}{\Gamma, A \otimes B \vdash C}$ $\frac{\Gamma \vdash A \quad \Delta, B \vdash C}{\Gamma, \Delta, A \multimap B \vdash C}$ $\frac{\Gamma, A \vdash B}{\Gamma \vdash A \multimap B}$

together with weakening and contraction of non-unique values:

$\frac{\Gamma \vdash A}{\Gamma, B^\ast \vdash A}$ $\frac{\Gamma, A^\ast, A^\ast \vdash B}{\Gamma, A^\ast \vdash B}$

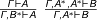
$\frac{\Gamma \vdash A}{\Gamma, B^\ast \vdash A}$ $\frac{\Gamma, A^\ast, A^\ast \vdash B}{\Gamma, A^\ast \vdash B}$

Crucially, any unique type can be coerced to its non-unique counterpart. The same can only happen on the left of the turnstyle if the result is guaranteed to be non-unique. There is an interesting duality here with linear logic, where the ! has the following rules:

$\frac{\Gamma, A \vdash B}{\Gamma, !A \vdash B}$ $\frac{!\Gamma \vdash A}{!\Gamma \vdash !A}$

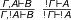
$\frac{\Gamma, A \vdash B}{\Gamma, !A \vdash B}$ $\frac{!\Gamma \vdash A}{!\Gamma \vdash !A}$

Thorsten remarked that where the rules for uniqueness type introduction and elimination form a monad, the linear types form a comonad.


comments powered by Disqus