Nottingham FP Lab Blog

Arrows as monoids

by Wouter on May 20, 2006.
Tagged as: Lunches.

With a little help from my more categorically inclined friends, I talked through some of the ideas in the recent paper by Chris Heunen and Bart Jacobs.

One way of describing a monad is as a monoidal structure in the category of endofunctors $\mathbf{C} \to \mathbf{C}$ . The unit of the monoid is of course the return; the binary operation is the join.

Now you can wonder whether there is a similar description of arrows. Quite interestingly, arrows can be described as monoids in the category 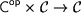$\mathcal{C}^{\text{op}} \times \mathcal{C} \to \mathcal{C}$ . Here the category 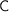$\mathbf{C}$ has to be cartesian closed and the functors have to be suitably strong, costrong, and internally strong. The arrow operation on objects extends naturally to a functor, very similar to the definition of hom-functors.

So what should the monoidal structure consist of? In the case of monads, we had a fairly canonical choice: the identity endofunctor and composition of endofunctors. As we now have bifunctors, we need to do a bit more work. Fortunately, the arrow operations give us some kind of clue. It turns out that the unit of the monoid consists of the arr operation taking exponential objects to arrows. To use arrow composition we need to construct a large coproduct and take a suitable coequalizer – which Neil pointed out was a coend.

The discussion then diverged into possible generalisations of arrows and enriched categories.