Nottingham FP Lab Blog
Bart Jacobs’ question (FP lunch 19/1/07)
by Thorsten on January 21, 2007.
Tagged as: Lunches.
Recently, Bart Jacob’s asked me a question about containers: He is looking for a formula for the derivative of a quotient container. I sketched a possible answer (I haven’t yet checked the details) and used this opportunity to give a quick introduction to containers.
A container is given by a set  of shapes and a family
of shapes and a family 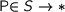 of position, giving rise to a functor
of position, giving rise to a functor
 given by
given by 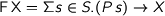 . It’s derivative as a functor is
. It’s derivative as a functor is
 . A quotient container is specified by additionally
. A quotient container is specified by additionally
giving a family of subgroups 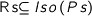 of the isomorphism group, it gives rise to a functor
of the isomorphism group, it gives rise to a functor
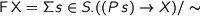 where the equivalence relation is generated by
where the equivalence relation is generated by 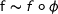 for
for
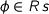 . I believe that it’s derivative is given by extending the previous formula by additionally specifying
. I believe that it’s derivative is given by extending the previous formula by additionally specifying
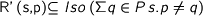 where
where 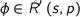 iff
iff  is given by restricting an isomorphim
is given by restricting an isomorphim 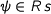 with the property
with the property 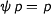 (by restricting I mean that
(by restricting I mean that  ).
).
comments powered by Disqus