Nottingham FP Lab Blog

Composing Applicative and Alternative

by Conor on July 8, 2007.
Tagged as: Lunches.

Nicolas asked whether the composition (either way around) of an Applicative functor

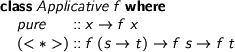
> class Applicative f where > pure :: x -> f x > (<*>) :: f (s -> t) -> f s -> f t

and an Alternative functor

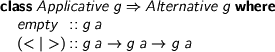
> class Applicative g => Alternative g where > empty :: g a > (<|>) :: g a -> g a -> g a

was necessarily Alternative (of course, both f⋅g and g⋅f are Applicative). The answer is yes, both are Alternative. Firstly, g⋅f is Alternative, just by specialising g’s operations. Secondly, f⋅g is Alternative just by the usual idiomatic f-lifting of g’s operations. The applicative functor laws guarantee that the f-effects are combined associatively.

In the hunt for interesting non-monadic examples, we were drawn once again to

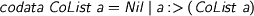
> codata CoList a = Nil | a :> (CoList a)

These things are not monadic like lists-with-‘nondeterminism’: the join
is not productive (what should 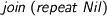|join (repeat Nil)| do? These things are not monadic like streams-with-‘diagonal’ (raggedness breaks associativity of joining). But they are Applicative in the ‘minimum-diagonal’ sense

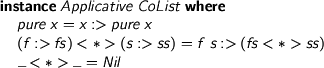
> instance Applicative CoList where > pure x = x :> pure x > (f :> fs) <*> (s :> ss) = f s :> (fs <*> ss) > _ <*> _ = Nil

They are also alternative

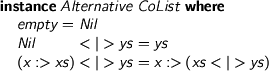
> instance Alternative CoList where > empty = Nil > Nil <|> ys = ys > (x :> xs) <|> ys = x :> (xs <|> ys)