Nottingham FP Lab Blog

Decisive Functors

by Conor on July 8, 2007.
Tagged as: Lunches.

It’s another name-choosing exercise that I’m vacillating about, but here’s today’s terminology for the dual to Applicative functors. Remember we had the lax monoidal presentation

> class Functor f => Applicative f where > unit :: () -> f () > mult :: (f s, f t) -> f (s, t)

> class Functor f => Applicative f where > unit :: () -> f () > mult :: (f s, f t) -> f (s, t)

Well, switch from products to coproducts and flip round those arrows and you’ve got

> class Functor f => Decisive f where > nogood :: f Zero -> Zero > orwell :: f (Either s t) -> Either (f s) (f t)

> class Functor f => Decisive f where > nogood :: f Zero -> Zero > orwell :: f (Either s t) -> Either (f s) (f t)

A Decisive f gives us some sort of certainty with respect to its parameter. If you think of f as some sort of epistemic modality, then it’s quite a useful one. Firstly, if we know/believe/imagine Zero, that must mean the world really is no good, and there really is an element of Zero. Even better, if we know/believe/imagine S or T, that must mean we actually know/believe/imagine S or know/believe/imagine T. ‘Or’ behaves well, and always gives us a decision.

I wonder what we expect to hold. Well, naturally,

> either (fmap g) (fmap h) . orwell = orwell . fmap (either g h)

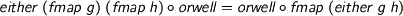
> either (fmap g) (fmap h) . orwell = orwell . fmap (either g h)

but surely we’d also like

> orwell . fmap Left = Left > orwell . fmap Right = Right
> either id orwell . orwell . fmap eassoc > = eassoc . either orwell id . orwell

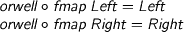
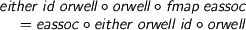
where

> eassoc :: Either (Either a b) c -> Either a (Either b c) > either :: (a -> c) -> (b -> c) -> Either a b -> c

> eassoc :: Either (Either a b) c -> Either a (Either b c) > either :: (a -> c) -> (b -> c) -> Either a b -> c

but we’d also hope for

> either (magic . nogood) id . orwell = fmap (either magic id) > either id (magic . nogood) . orwell = fmap (either id magic)

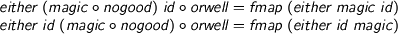
> either (magic . nogood) id . orwell = fmap (either magic id) > either id (magic . nogood) . orwell = fmap (either id magic)

I wonder what else.

There’s an ‘idiomatic’ interface to these things.

> class Functor f => Decisive f where > refute :: f Zero -> a > branch :: (f s -> a) -> (f t -> a) -> f (Either s t) -> a

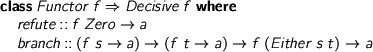
> class Functor f => Decisive f where > refute :: f Zero -> a > branch :: (f s -> a) -> (f t -> a) -> f (Either s t) -> a

Now, guess what. Every comonad is decisive. As it were,

> instance Comonad c => Decisive c where > nogood = counit > orwell story = case counit story of > Left s -> fmap (either id (const s)) story > Right t -> fmap (either (const t) id) story

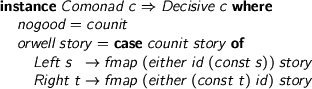
> instance Comonad c => Decisive c where > nogood = counit > orwell story = case counit story of > Left s -> fmap (either id (const s)) story > Right t -> fmap (either (const t) id) story

That is, orwell revises the story so that, throughout, it’s consistently on whichever side we happen to be on at the (counit) moment.


comments powered by Disqus