Nottingham FP Lab Blog

Nonempty Lists and Padding

by Conor on July 8, 2007.
Tagged as: Lunches.

Lists are applicative with a zipping-truncating behaviour, but these guys (written backwards, today)

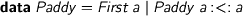
> data Paddy = First a | Paddy a :<: a

are applicative with a zipping-padding behaviour. Like this

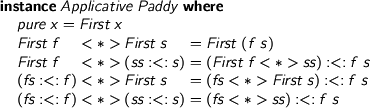
> instance Applicative Paddy where > pure x = First x > First f <*> First s = First (f s) > First f <*> (ss :<: s) = (First f <*> ss) :<: f s > (fs :<: f) <*> First s = (fs <*> First s) :<: f s > (fs :<: f) <*> (ss :<: s) = (fs <*> ss) :<: f s

They're also happily monadic in the nondeterministic sense. Moreover, the join

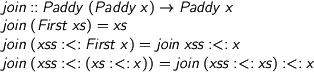
> join :: Paddy (Paddy x) -> Paddy x > join (First xs) = xs > join (xss :<: First x) = join xss :<: x > join (xss :<: (xs :<: x)) = join (xss :<: xs) :<: x

is structurally recursive (if you know what you're doing) and structurally corecursive, unlike the obvious candidate for join on CoList.

So these guys, as data or codata, get to be monadic hence applicative, but also (and differently) zip-max applicative. The padding behaviour is useful for making rectangular text boxes.

Note that Paddy is not Alternative because, like Ernst Stavro Blofeld, he doesn't tolerate failure.

However, Paddy is also comonadic.

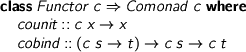
> class Functor c => Comonad c where > counit :: c x -> x > cobind :: (c s -> t) -> c s -> c t

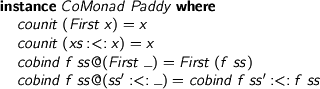
> instance CoMonad Paddy where > counit (First x) = x > counit (xs :<: x) = x > cobind f ss@(First _) = First (f ss) > cobind f ss@(ss' :<: _) = cobind f ss' :<: f ss

That's to say, thinking of these things temporally, each entry in the output to a cobind at a given time is given by the history of the input up to that time. Computations can't do more, but they can be more, by being in context. Again, note productivity means the codata version is also comonadic.

Reminder: lists, colists, etc are not instances of the free/completely iterative monad/comonad construction, as they have node information rather than leaf information, and are additive. Amusing, then, that they are so well behaved.