Nottingham FP Lab Blog

Peano induction for binary numbers (bis)

by Conor on August 7, 2007.
Tagged as: Lunches.

This is a story from the early days of designing Epigram. It’s a case study of equipping a data structure with a funny induction principle. I want to show that a binary representation of positive numbers satisfies a unary induction principle. I think I got the problem from Nicolas Magaud a while back, but Hugo Herbelin reminded me of it at CHIT/CHAT, so I dug it out of my bottom drawer. I’ll be informal, tending to Agda, notationally.

Positive binary numbers are snoc-lists of bits with a 1 at the front.

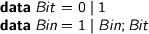
> data Bit = 0 | 1 > data Bin = 1 | Bin;Bit

We can easily write their successor operation by structural recursion.

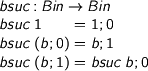
> bsuc : Bin -> Bin > bsuc 1 = 1 ; 0 > bsuc (b ; 0) = b ; 1 > bsuc (b ; 1) = bsuc b ; 0

Now the task is to give

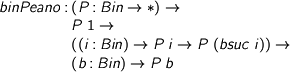
$%format forall = “\forall” > binPeano : (P : Bin -> *) -> > P 1 -> > ((i : Bin) -> P i -> P (bsuc i)) -> > (b : Bin) -> P b$

%format forall = “\forall” > binPeano : (P : Bin -> *) -> > P 1 -> > ((i : Bin) -> P i -> P (bsuc i)) -> > (b : Bin) -> P b

I’ll give a broken attempt, followed by my proof, and then James McKinna’s proof.

Let’s try fixing P and its closure properties, then proceeding by structural recursion on b.

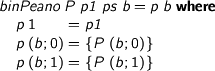
> binPeano P p1 ps b = p b where > p 1 = p1 > p (b ; 0) = {P (b ; 0)} > p (b ; 1) = {P (b ; 1)}

Now what? In the ‘even’ case, we can get our hands on p b : P b, but we need to show P (b ; 0), so we need to do a successor step b times. If only we knew how to iterate b times…but that’s what we’re trying to achieve in the first place. Arse!

So let’s try again, except that instead of trying to prove P, let’s try to establish ability to iterate. I’ll move b to the front, and keep P inside the induction.

$%format forall = “\forall” > binPeano : (b : Bin) -> > (P : Bin -> *) -> > P 1 -> > ((i : Bin) -> P i -> P (bsuc i)) -> > P b > > binPeano 1 P p1 ps = p1 > binPeano (b ; 0) P p1 ps = binPeano b (\b -> P (b ; 0)) > {P (1 ; 0)} > {(i : Bin) -> P (i ; 0) -> P (bsuc i ; 0)} > binPeano (b ; 1) P p1 ps = binPeano b (\b -> P (b ; 1)) > {P (1 ; 1)} > {(i : Bin) -> P (i ; 1) -> P (bsuc i ; 1)}$

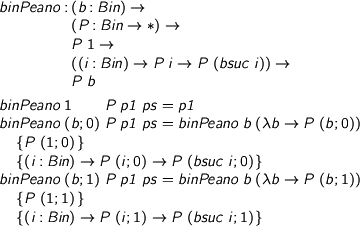
%format forall = “\forall” > binPeano : (b : Bin) -> > (P : Bin -> *) -> > P 1 -> > ((i : Bin) -> P i -> P (bsuc i)) -> > P b > > binPeano 1 P p1 ps = p1 > binPeano (b ; 0) P p1 ps = binPeano b (\b -> P (b ; 0)) > {P (1 ; 0)} > {(i : Bin) -> P (i ; 0) -> P (bsuc i ; 0)} > binPeano (b ; 1) P p1 ps = binPeano b (\b -> P (b ; 1)) > {P (1 ; 1)} > {(i : Bin) -> P (i ; 1) -> P (bsuc i ; 1)}

What has happened here? By keeping P inside the induction, we’ve turned it into what ripplers would call a ‘sink’ capable of absorbing the differences between the induction hypothesis and the induction conclusion. And that’s how we use it: to prove P of twice b, prove (P of twice) b! The remaining holes are pretty easy to fill, for (bsuc i ; 0) is exactly bsuc (bsuc (i ; 0)), and so on. To finish the job, we need to establish the base cases, then do a double step. That is, to iterate (twice b) times, do a double step b times.

$%format forall = “\forall” > binPeano : (b : Bin) -> > (P : Bin -> *) -> > P 1 -> > ((i : Bin) -> P i -> P (bsuc i)) -> > P b > > binPeano 1 P p1 ps = p1 > binPeano (b ; 0) P p1 ps = binPeano b (\b -> P (b ; 0)) > (ps p1) > (\i -> ps (i ; 1) . ps (i ; 0)) > binPeano (b ; 1) P p1 ps = binPeano b (\b -> P (b ; 1)) > (ps (ps p1)) > (\i -> ps (bsuc i ; 0) . ps (i ; 1))$

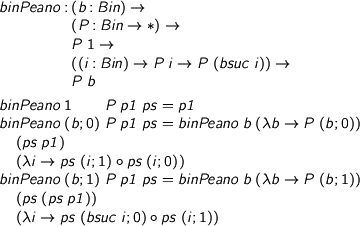
%format forall = “\forall” > binPeano : (b : Bin) -> > (P : Bin -> *) -> > P 1 -> > ((i : Bin) -> P i -> P (bsuc i)) -> > P b > > binPeano 1 P p1 ps = p1 > binPeano (b ; 0) P p1 ps = binPeano b (\b -> P (b ; 0)) > (ps p1) > (\i -> ps (i ; 1) . ps (i ; 0)) > binPeano (b ; 1) P p1 ps = binPeano b (\b -> P (b ; 1)) > (ps (ps p1)) > (\i -> ps (bsuc i ; 0) . ps (i ; 1))

So that’s that, except that it’s a bit tricky and a bit higher-order and, worst of all, quite expensive in the size of the inductions involved. If we’re being scrupulous about universe levels, we have to be careful about quantifying over arbitrary P : Bin -> Set_i. To be allowed such a thing, we need to use our structural induction principle at Set_(i+1). Pricey! But with universe polymorphism (if only we had it) ok.

Then along comes James McKinna and shows us how to keep it first-order and small, all the way along. Instead of working with arbitrary predicates closed under 1 and bsuc, work with the smallest such predicate, as it implies the others. What’s the smallest? Why, the inductively defined predicate!

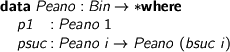
> data Peano : Bin -> * where > p1 : Peano 1 > psuc : Peano i -> Peano (bsuc i)

Now, the weak rule induction principle for Peano is exactly the induction principle we want, except that it imposes the precondition that Peano should actually hold, of course. Our mission is now to show that it does.

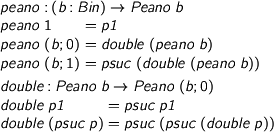
> peano : (b : Bin) -> Peano b > peano 1 = p1 > peano (b ; 0) = double (peano b) > peano (b ; 1) = psuc (double (peano b)) > > double : Peano b -> Peano (b ; 0) > double p1 = psuc p1 > double (psuc p) = psuc (psuc (double p))

And we’re done. James and I liked this trick so much, we designed a programming language to exploit it. That’d be Epigram.

Recent FP lunches, as well as conversations with James McKinna, Randy Pollack, Lucas Dixon, Roy McCasland, Alan Bundy and J Strother Moore have me thinking again about this stuff. Watch this space…