Nottingham FP Lab Blog
Proof by Smugness
by Conor on August 7, 2007.
Tagged as: Lunches.
Last Friday, shortly after my return from Edinburgh, I gave a slappably smug talk, in an infuriating up-the-garden-path style, about an idea which was provoked by James McKinna, and by which I was somewhat tickled. It’s an exploration of the freedom you get with dependent types to shift where you draw the line between building hygiene conditions into the structure of your data, thus preventing certain kinds of error a priori, and verifying that your programs satisfy laws a posteriori.
James reminded me of the compiler correctness story (McKinna and Wright, to appear in JFP). He and Joel showed how to compile a simple expression language into ‘bytecode’ for a stack machine. The datatype of code guaranteed operand compatibility and prevented underflow, making it easier to give its semantics. The proof that the compiled code was correct with respect to the evaluation function was done later. James asked me what would happen if we tried to build compiler correctness, not just stack safety, into the types. Guess what…?
So here goes, in Agda. Of course, I’m just going to do this for Hutton’s Razor,
because if you can’t do whatever it is for Hutton’s Razor, it isn’t going to be much use. We have Nat and + as usual, then
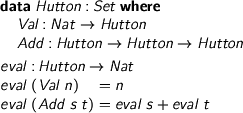
> data Hutton : Set where > Val : Nat -> Hutton > Add : Hutton -> Hutton -> Hutton > > eval : Hutton -> Nat > eval (Val n) = n > eval (Add s t) = eval s + eval t
That’s our tiny language and its reference semantics. Now let’s have our machine code. I cheat slightly by having tree-structured code, but flattening can happen separately, another time. The idea is to index code by initial and final stack configuration and that way to ensure stack safety. Here, we only have one sort of stack entry, so a configuration is just a height.
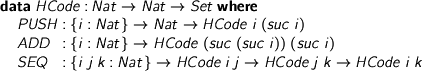
> data HCode : Nat -> Nat -> Set where > PUSH : {i : Nat} -> Nat -> HCode i (suc i) > ADD : {i : Nat} -> HCode (suc (suc i)) (suc i) > SEQ : {i j k : Nat} -> HCode i j -> HCode j k -> HCode i k
See? PUSH increments height; ADD requires two operands; SEQ joins up nicely in the middle. I skipped SKIP, but you can add it yourself.
Now, given some HCode i j, you can interpret it as a stack transformation—a function in Sem i j where
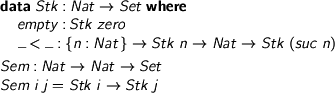
> data Stk : Nat -> Set where > empty : Stk zero > _<_ : {n : Nat} -> Stk n -> Nat -> Stk (suc n) > > Sem : Nat -> Nat -> Set > Sem i j = Stk i -> Stk j
To write this interpreter, implement the operations of HCode for Sem. That is, give an HCode-algebra with Sem as its carrier, making the interpreter a fold (catamorphism, in 2.1-Greek). Let’s write down the general pattern, then instantiate it. First, what’s an algebra?
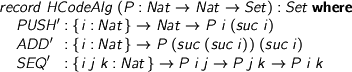
> record HCodeAlg (P : Nat -> Nat -> Set) : Set where > PUSH' : {i : Nat} -> Nat -> P i (suc i) > ADD' : {i : Nat} -> P (suc (suc i)) (suc i) > SEQ' : {i j k : Nat} -> P i j -> P j k -> P i k
It’s a record, parametrised by a carrier type family with the same index structure as HCode itself. Its fields correspond to HCode’s constructors. I’ve quietly done the Agda voodoo to expose these fields as projection functions, and now I can write the fold:
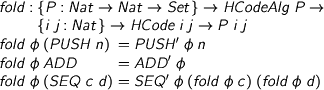
%format phi = “\phi” > fold : {P : Nat -> Nat -> Set} -> HCodeAlg P -> > {i j : Nat} -> HCode i j -> P i j > fold phi (PUSH n) = PUSH' phi n > fold phi ADD = ADD' phi > fold phi (SEQ c d) = SEQ' phi (fold phi c) (fold phi d)
As normal, fold replaces the constructor THING with the semantics THING’ φ from the algebra. That much is completely determined by the structure of HCode. The creative bit is the algebra for our semantics:
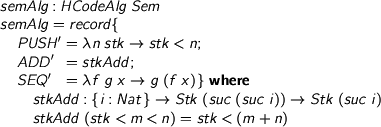
> semAlg : HCodeAlg Sem > semAlg = record { > PUSH' = \n stk -> stk < n; > ADD' = stkAdd; > SEQ' = \f g x -> g (f x) } where > stkAdd : {i : Nat} -> Stk (suc (suc i)) -> Stk (suc i) > stkAdd (stk < m < n) = stk < (m + n)
Now the challenge is to build correctness into code as well. So here's the idea: give a datatype of code with semantic markup, then write the compiler with respect to the reference semantics. Guess what? An algebra induces a marked-up version of a datatype.

%format phi = “\phi” > data HCodeM {P : Nat -> Nat -> Set}(phi : HCodeAlg P) > : (i j : Nat) -> P i j -> Set where > PUSHM : {i : Nat} -> (n : Nat) -> > HCodeM phi i (suc i) (PUSH' phi n) > ADDM : {i : Nat} -> > HCodeM phi (suc (suc i)) (suc i) (ADD' phi) > SEQM : {i j k : Nat}{a : P i j}{b : P j k} -> > HCodeM phi i j a -> HCodeM phi j k b -> > HCodeM phi i k (SEQ' phi a b)
All I’ve done is to label each constructor of HCode with its semantics, using the given algebra to calculate the semantics of the whole from the semantics of the part. That’s just mechanical. Equally mechanical is the forgetful operation which throws away the markup.
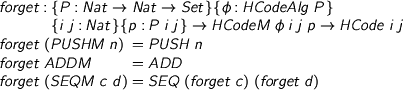
%format phi = “\phi” > forget : {P : Nat -> Nat -> Set}{phi : HCodeAlg P} > {i j : Nat}{p : P i j} -> HCodeM phi i j p -> HCode i j > forget (PUSHM n) = PUSH n > forget ADDM = ADD > forget (SEQM c d) = SEQ (forget c) (forget d)
Even if we forget the markup, we can still recover the semantics by computing it recursively with fold. Again, we (morally) have for free that that the semantic markup tells you what happens if you run the code.
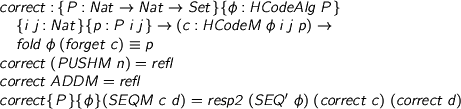
%format phi = “\phi” %format == = “\equiv” > correct : {P : Nat -> Nat -> Set}{phi : HCodeAlg P} > {i j : Nat}{p : P i j} -> (c : HCodeM phi i j p) -> > fold phi (forget c) == p > correct (PUSHM n) = refl > correct ADDM = refl > correct {P} {phi} (SEQM c d) = resp2 (SEQ' phi) (correct c) (correct d)
where ≡ is propositional equality, refl its reflexivity property and resp2 the proof that two-argument functions respect ≡. It should come as no surprise that this holds: I designed the markup to make this true.
Now let’s write a correct compiler. First we write the core of the thing, producing marked up code with the right semantics.
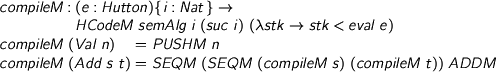
> compileM : (e : Hutton){i : Nat} -> > HCodeM semAlg i (suc i) (\stk -> stk < eval e) > compileM (Val n) = PUSHM n > compileM (Add s t) = SEQM (SEQM (compileM s) (compileM t)) ADDM
That code just typechecks! Now, to produce actual code, forget the markup:
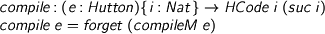
> compile : (e : Hutton){i : Nat} -> HCode i (suc i) > compile e = forget (compileM e)
But now we have correctness on a plate!
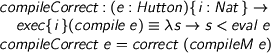
%format == = “\equiv” > compileCorrect : (e : Hutton){i : Nat} -> > exec {i} (compile e) == \s -> s < eval e > compileCorrect e = correct (compileM e)
So I was able to write the compiler-you-first-thought-of and get its correctness pretty much for free. How was that? Well, the usual proof is an induction on the execution of the code, with a mixture of partial evaluation (which we get for free) and rewriting by the inductive hypothesis (which is what was being set up by my construction of HCodeM). Rather than writing a recursive program and then doing an inductive proof exactly following its structure, I glued the two together. If the proof plan was more complex, appealing to other equational laws, perhaps, I’d have to use equational reasoning to show that the markup fits together properly. This example is simple enough that I get away with it.
See what other examples of proof by smugness you can find!
comments powered by Disqus