Nottingham FP Lab Blog

Parametricity

by Thorsten on January 26, 2008.
Tagged as: Lunches.

Triggered by Paul Levy’s recent post on the TYPES mailing list (and my reply) I reviewed the concept of parametricity for System F. First I talked about impredicative encodings: In System F, any type 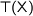T(X) with a positive occurence of a type variable 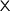gives rise to a functor, i.e. there is a term 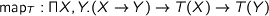$map_T : \Pi X,Y.(X\to Y)\to T(X) \to T(Y)$ , and we can construct a weakly initial algebra 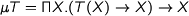$\mu T = \Pi X.(T(X)\to X)\to X$ with the structure map 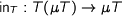$in_T : T(\mu T)\to \mu T$ by
$in_T = \lambda t:T(\mu T).\lambda X,f:T(X)\to X.f (map_T (\lambda n:\mu T.n X f) t)$ .
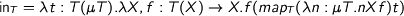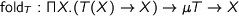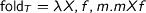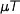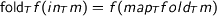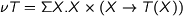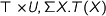The fold operation $fold_T : \Pi X.(T(X)\to X) \to \mu T \to X$ is simply $fold_T = \lambda X,f,m.m X f$ since the type of fold motivated this encoding. It is easy to see that $\mu T$ is weakly initial because fold_T f (in_T m) = f (map_T fold_T m) . This also dualizes to weakly terminal coalgebras $\nu T = \Sigma X.X\times (X \to T(X))$ where $T \times U,\Sigma X.T(X)$ can be encoded impredicatively as 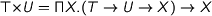$T\times U = \Pi X.(T \to U \to X) \to X$ and $\Sigma X.T(X) = \Pi Y.(Pi X.T(X)\to Y)\to Y$ .

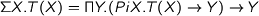To show that these encodings are strong, we need the additional assumption of parametricity. For any type 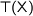T(X) we give a relational interpretation, which assigns to 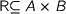$R\subseteq A\times B$ a relation 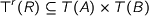$T^{r}(R) \subseteq T(A)\times T(B)$ — I am simplifying here since we have to interpret types with any number of free variables. This is given by
$\begin{eqnarray*}x X^r(R) y & = & x R y\\ f (T \to U)^r(R) g & = & \forall x,y.x T^r(R) y \to f x U^r(R) g y\\ f (\Pi X.T(X))^r g & = & \forall A,B,R\subseteq A\times B. f A T^r(R) g B \end{eqnarray*}$
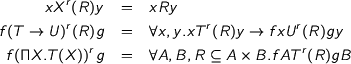
Parametricity means that every closed 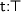t:T is related to itself t T^r t .

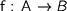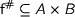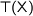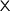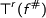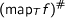An important lemma is the map-property which relates the relational and functorial properties of types. Any function $f : A \to B$ gives rise to a relation $f^\# \subseteq A\times B$ . Now given a type T(X) with a positive occurence of we can show that $T^r(f^\#)$ and $(map_T f)^\#$ agree.

As Phil Wadler noticed we can derive initiality from parametricity for 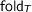fold_T . Interestingly, we have to use parametricity twice! Parametricity for fold implies that fold is natural, i.e. given two T-algebras 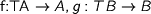$f:TA \to A, g: TB \to B$ and a T-algebra morphism 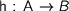$h : A \to B$ , s.t. 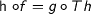$h \circ f = g \circ T h$ , this entails that 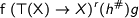$f (T(X) \to X)^r(h^\#) g$ . Assuming parametricity we obtain that 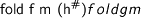$fold f m (h^{\#}) fold g m$ for any 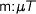$m:\mu T$ , i.e.
fold_T g m = h (fold_T f m) .

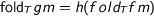Initiality means that for any 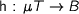$h : \mu T \to B$ such that 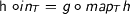$h \circ in_T = g \circ map_T h$ it holds that 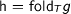h = fold_T g . This is indeed a consequence of the naturality of fold if we instantiate f = in_T , the precondition follows from weak initiality. However, it remains to show that 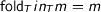fold_T in_T m = m . Interestingly, this also follows from naturality using 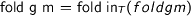fold g m = fold in_T (fold g m) . From here, 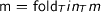m = fold_T in_T m follows by unfolding fold and applying 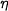$\eta$ -equality.

Paul asked whether 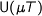$U(\mu T)$ is isomorphic to $Pi X.(T(X)\to X)\to U(X)$ , where both T,U have positive occurences of a type variable X. Indeed, I have now checked that this follows by adapting the reasoning above and using the map property of U as well.