Nottingham FP Lab Blog
FP -vs- OO bialgebraically (“Expression Lemma”)
by Ondrej on February 22, 2008.
Tagged as: Lunches.
Today I showed how distributive laws of a monad over a comonad and adequacy results for bialgebraic operational semantics [Plotkin & Turi] can be used to formalize the correspondence between (certain) FP algebraic datatypes with functions (essentially implementations of abstract data types) and recursive OO structures (collections of classes with the same interface).
In short, given a functor 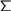 standing for the signature of a datatype and a (finite) collection of functions
standing for the signature of a datatype and a (finite) collection of functions  (where
(where 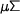 is the least fixed point of
is the least fixed point of 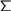 and each
and each 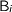 is a functor), we can form the tupple
is a functor), we can form the tupple  . Let
. Let 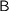 be defined as the product
be defined as the product 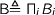 . This arrow
. This arrow  is quite often a catamorphism whose algebra factors through a natural transformation
is quite often a catamorphism whose algebra factors through a natural transformation 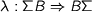 , thus
, thus 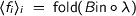 , where
, where 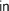 is the initial
is the initial 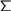 -algebra. Informally,
-algebra. Informally, 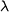 here combines recursive results from subterms and
here combines recursive results from subterms and 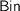 packs recursive results into a new instance of
packs recursive results into a new instance of 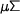 (for instance in a catamorphically defined map).
(for instance in a catamorphically defined map).
On the other hand, let us take the colagebraic view of objects [e.g. Jacobs] where interfaces are (certain) polynomial endofunctors, classes are coalgebras and object types are carriers of terminal coalgebras. Then a collection of classes with the same interface, 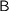 , whose carriers are respectively given by the cases of the algebraic datatype functor
, whose carriers are respectively given by the cases of the algebraic datatype functor 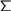 are defined by a single coalgebra
are defined by a single coalgebra 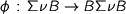 (where
(where 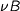 is the greatest fixed point of
is the greatest fixed point of 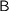 , i.e. the carrier of the terminal
, i.e. the carrier of the terminal 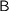 -coalgebra). Let us take
-coalgebra). Let us take 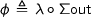 . This corresponds to the classes recursively delegating to their subcomponents and then combining the resulting collection of behaviours into a behaviour on a collection.
. This corresponds to the classes recursively delegating to their subcomponents and then combining the resulting collection of behaviours into a behaviour on a collection.
Now 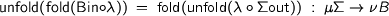 . This means that the functional program defined by a fold over an algebraic datatype, when wrapped up as an abstract datatype with interface
. This means that the functional program defined by a fold over an algebraic datatype, when wrapped up as an abstract datatype with interface 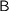 , is bisimilar to the object constructed by folding a class constructor over a tree of object states. Note that in the latter case, each layer is first turned into a collection of objects (by
, is bisimilar to the object constructed by folding a class constructor over a tree of object states. Note that in the latter case, each layer is first turned into a collection of objects (by 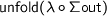 ) which are then used to construct an object at the next level (as common in OO). In the first functional case, the functions are defined directly on an open datatype and the whole result is then interpreted as an abstract data type (object).
) which are then used to construct an object at the next level (as common in OO). In the first functional case, the functions are defined directly on an open datatype and the whole result is then interpreted as an abstract data type (object).
The situation generalizes straightforwardly for more general distributive laws of a monad over a comonad, in particular when the monad is free and comonad cofree. Thus 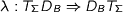 . This allows us to express a larger class of OO and FP programs while still preserving their bisimilarity.
. This allows us to express a larger class of OO and FP programs while still preserving their bisimilarity.
A paper about this has been recently submitted for conference publication. The preliminary version and some relevant Haskell implementation can be found here.
comments powered by Disqus