Nottingham FP Lab Blog

Recursion with boxes

by Thorsten on June 21, 2008.
Tagged as: Lunches.

While recursion in conventional functional languages is well understood, i.e. we know how to typecheck and how to run recursive programs it is more of an issue for languages with dependent types. The reason is that a typechecker for a dependently typed language has to evaluate terms symbolically (i.e. in the presence of variables) and has to decide definitional equality, i.e. 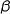the equality generated by $\alpha$ and $\beta$ -rules and by unfolding (recursive) definitions.

The main problem is how to stop infinite unfolding of recursive definitions. If we accept that $\mathrm{let}\,x=t\,\mathrm{in}\,u \equiv \mathrm{let}\,x=t\,\mathrm{in}\,u[x:=t]$ and 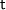contains occurences of we can continue to unfold forever. This applies even to the recursive definitions of completely innocent total functions such as addition, e.g.
$\mathrm{let}\, add\, =\, \lambda m\, n \to\, \mathrm{case}\, m\, \mathrm{of} 0 \Rightarrow\, n \mid S\, m' \Rightarrow\, S(add\,m'\,n)\, \mathrm{in}\, add\, 3\, 4$

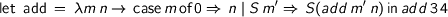
This issue is avoided in systems like Coq or Agda by restricting the evaluation of recursive definitions to certain contexts. E.g while the recursive definition of 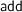add is unfolded in 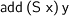$add\,(S x)\,y$ because 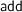add is applied to a term in constructor form, it is not unfolded in the context $add\,x\,y$ .

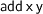However, this approach has a number of disadvantages: it means that evaluation and pattern matching is built into the core language (Another alternative is to translate recursive definitions into basic combinators of Type Theory – this is the approach taken in Epigram). If we want to extend the language to corecursion we have to modify the notion of evaluation contexts, and indeed Coq makes a difference between fix and cofix. Moreover, a different mechanism is used to express the recursive definition of types, which has further to be extended if we want to capture induction-recursion, i.e. the mutual recursive definition of a type and a function.

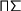Nicolas Oury and I have recently proposed a different approach in our draft paper on $\Pi\Sigma$ (recently rejected from ICFP). in $\Pi\Sigma$ we restrict the unfolding of recursion by the use of boxes. In a boxed term recursive definitions from outside the box are not unfolded. E.g. $\mathrm{let}\,x=t\,\mathrm{in}\,[x]\not\equiv \mathrm{let}\,x=t\,\mathrm{in}\,[t]$ . In his recent work on the calculus of definitions Thierry Coquand proposes a similar approach, restricting the unfolding of recursive definition in finite functions corresponding to case-expressions. 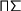This behaviour can be simulated in $\Pi\Sigma$ by using boxes in the branches of case-expression.

If we are not careful when introducing boxes we may loose desriable properties of our languages, such as subject reduction. Nicolas’ example from the recent FP lunch discussion, can also be simulated in 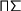$\Pi\Sigma$ , it seems. We define recursively a type of Streams:
Stream : Type. Stream = tag : {'Cons} ; Case tag of {'Cons -> $ Stream }.
here the $ A is the ASCII notation for lifting 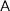$A_\bottom$ . We define recursively
ticks : Stream. ticks = 'Cons, [ticks].
Currently 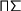$\Pi\Sigma$ hasn’t got a primitive equality type but we can just define Leibniz equality:
Eq : (A : Type) -> A -> A -> Type. Eq = \ A -> \ a -> \ b -> (P : A -> Type) -> P a -> P b.

refl : (A : Type) -> (a : A) -> Eq A a a.
refl = \ A -> \ a -> \ P -> \ p -> p.

We can show:
l1 : Eq Stream ticks ('Cons, [ticks]). l1 = refl Stream ticks.
We can also show that the recursive functional is a congruence:
l2 : (s : Stream) -> (t : Stream) -> (Eq Stream s t) -> Eq Stream ('Cons, [s]) ('Cons, [t]) l2 = \ s -> \ t -> \ q -> \ P -> \ p -> q (\ x -> P ('Cons,x)) p.
Putting l1 and l2 together we seem to be able to unfold inside a box
l3 : Eq ('Cons, [ticks]) ('Cons, [('Cons, [ticks])]). l3 = l2 ticks ('Cons, [ticks]) l1.
However, if we reduce l3 to normal form it is basically an instance of refl, i.e.
\ P -> \ p -> p and this has not got l3′s type because
the expressions ('Cons, [ticks]) and ('Cons, [('Cons, [ticks])]) are not convertible. Clearly we have lost subject reduction.

In an email Thierry pointed out that the calculus of definitions doesn’t have this problem, and indeed neither should have 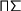$\Pi\Sigma$ . The problem is caused by being half-hearted: we say that boxes are opaque for recursive definitions, but they are transparent for substitutions or non-recursive definitions. If we are consequent, i.e. boxes are opaque, full stop, the problem seems to disappear. I.e. the 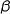$\beta$ -rule becomes 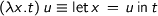$(\lambda x.t)\,u \equiv \mathrm{let}\,x\,=\,u\,\mathrm{in}\,t$ . If we adopt this principle, l2 isn’t provable: while equality is a congruence, we can not reduce let x=s in ('Cons,[x]) to ('Cons,[s]).

Introducing boxes raises some further questions: should boxes be stable under $\alpha$ -equivalence? E.g. should $\mathrm{let}\,x\,=\,3\,\mathrm{in}\,[x] \equiv \mathrm{let}\,y\,=\,3\,\mathrm{in}\,[y]$ ? Should it be stable under weakening? E.g.
$\mathrm{let}\,x\,=\,3\,\mathrm{in}\,[4] \equiv [4]$ ? And under permutation of definitions? E.g. should $\mathrm{let}\,x\,=\,3, y\,=\,4\,\mathrm{in}\,[(x,y)]\equiv \mathrm{let}\,x\,=\,4, y\,=\,3\,\mathrm{in}\,[(y,x)]$ ?
Inspired by the last example, we may even wonder, whether $\mathrm{let}\,x\,=\,3, y\,=\,3\,\mathrm{in}\,[(x,y)]\equiv \mathrm{let}\,x\,=\,3\,\mathrm{in}\,[(x,x)]$ ?

We propose that all the equivalence but the last should hold. We say that two local definitions are $\alpha$ -equivalent, if there is a partial bijection on the defined variables, such that the right-hand sides and also the body are identified. While opaque to local definitions, boxes should be stable under this sort of $\alpha$ -equivalence. The last example fails because the required identification is not bijective. Weakening is included, since the empty relation is a partial bijection.
(I have used partial bijections before to characterize $\alpha$ -equivalence, see the draft paper – but beware it does contain some bugs).

Nicolas already suggested a simple algorithm to decide this equivalence: when comparing a closure of a box, when comparing two defined variables, we replace them by their definitions, but substitute both by a new generic variables. This procedure clearly terminates because any recursive definition is at most unfolded once. It should also be at least intutively clear that this precisely implements the $\alpha$ -equivalence sketched above.