Nottingham FP Lab Blog

Modular Monad Transformers

by Mauro Jaskelioff on September 4, 2008.
Tagged as: Lunches.

Monad are an essential tool for functional programmers. When it comes to combining monads, the most popular technique is to use monad transformers to add an effect layer to an existing monad. Do you want a new state for your monad? Use the state monad transformer on your monad and voila! it’s done!

Actually, you are not really done. Monads usually come with a set of operations to manipulate the effect they model. For example, the state monad comes with operations for reading and updating the state (get and put), and the environment monad (Reader in Haskell) comes with operations for reading the environment and performing a computation in a modified environment (ask and local). If you want the operations of your monad to be supported by the transformed monad, then you need to show how to lift the operations to the transformed monad. Unless a technology is used for automating these liftings, you need to provide an operation instance for every monad transformer in the library, leading to 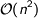$\mathcal{O}(n^2)$ operation instances. That’s not modular!

The problem is not in monad transformers (other technologies for combining monads such as distributive laws or coproduct of monads suffer from the same problem). The problem is that many of the operations associated with a monad are not really compatible with the monad.

Monads have axioms that ensure that return and bind are well-behaved, so it is not unreasonable to think that there should be some axioms associated to its operations. So I propose to require operations to be algebraic. In our context this means that an operation h for a monad M should be of type forall a . S (M a) -> M a for some functor S, such that:

join . h = h. fmap join

where join is the multiplication of the monad join = (>>= id).

For example, uncurry (++) :: ([a],[a]) -> [a] is algebraic for the list monad, with S a = (a,a). On the other hand, uncurry local :: (r->r, Reader r a) -> Reader r a has the correct type, with functor S a = (r -> r, a), but is not algebraic, as the condition does not hold. The operation ask :: Reader r r doesn’t seem to have the correct type, but it is isomorphic to a function ask' :: (r -> Reader r a) -> Reader r a, which is algebraic for Reader r with S a = r -> a. It’s convenient to consider algebraic operations up to isomorphism. Then, ask and (++) are algebraic.

So, what’s good about algebraic operations? They can be lifted by any monad morphism! Every algebraic operation is isomorphic to a natural transformation in the Kleisli category of the monad.

$%format . = “\cdot” \begin{code} toK :: (Functor s, Monad m) => (forall a. s (m a) -> m a) -> (forall a. s a -> m a) toK f = f . fmap return fromK :: (Functor s, Monad m) => (forall a. s a -> m a) -> (forall a. s (m a) -> m a) fromK k = join . k \end{code}$

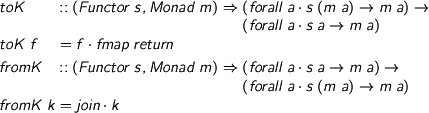
%format . = “\cdot” \begin{code} toK :: (Functor s, Monad m) => (forall a. s (m a) -> m a) -> (forall a. s a -> m a) toK f = f . fmap return fromK :: (Functor s, Monad m) => (forall a. s a -> m a) -> (forall a. s (m a) -> m a) fromK k = join . k \end{code}

This means that for every algebraic operation h :: forall a. S (M a) -> M a, monad N, and monad morphism lift :: forall a. M a -> N a, we get an algebraic operation fromK (lift. toK h) :: forall a. S (N a) -> N a, i.e. the lifting of h to N.

Append is algebraic for the list monad, so we get a “liftable” version of append: for every monad morphism out of the list monad, we get a lifted operation.

$%format . = “\cdot” \begin{code} appendL :: Monad m => (forall x. [x] -> m x) -> m a -> m a -> m a appendL mm x y = join $ mm $ return x ++ return y \end{code}$

%format . = “\cdot” \begin{code} appendL :: Monad m => (forall x. [x] -> m x) -> m a -> m a -> m a appendL mm x y = join $ mm $ return x ++ return y \end{code}

Of course, not all the usual operations are algebraic for their monad. This does not mean that the operation is incorrect, but that the monad should be more powerful. The operations determine the appropriate monad.

The operation local is not an algebraic for Reader but can become algebraic if we implement the environment monad with State:

$%format . = “\cdot” \begin{code} type Reader' r a = State r a reader' :: (r -> a) -> Reader' r a reader' e = State (\r -> (e r, r)) runReader' :: Reader' r a -> r -> a runReader' r = fst . runState r local' :: (r -> r) -> Reader' r a -> Reader' r a local' f a = join $ State $ \r -> (a, f r) localL :: Monad t => (forall x. Reader' r x -> t x) -> (r -> r) -> t a -> t a localL lift f t = join $ lift $ State (\r -> (t, f r)) \end{code}$

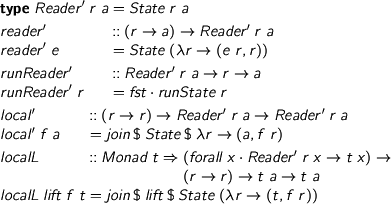
%format . = “\cdot” \begin{code} type Reader' r a = State r a reader' :: (r -> a) -> Reader' r a reader' e = State (\r -> (e r, r)) runReader' :: Reader' r a -> r -> a runReader' r = fst . runState r local' :: (r -> r) -> Reader' r a -> Reader' r a local' f a = join $ State $ \r -> (a, f r) localL :: Monad t => (forall x. Reader' r x -> t x) -> (r -> r) -> t a -> t a localL lift f t = join $ lift $ State (\r -> (t, f r)) \end{code}

Since local' is algebraic for Reader', we get a liftable operation localL. The apparently arbitrary move from Reader into State seems like a big eureka step. Actually, it’s the result of applying a general technique for finding appropriate monads for a given set of operations (paper in process).

Using these ideas, I managed to re-implement the monad transformer library with automatic lifting of operations. I will release the library as soon as I write a minimum of documentation.