Nottingham FP Lab Blog

Exponentials of containers (again)

by Thorsten on September 5, 2008.
Tagged as: Lunches.

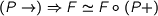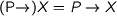I presented a simple derivation of Paul’s construction of the exponential of containers. I used the opportunity to discuss the exponential of functors and the Yoneda lemma. My derivation is based on the observation that $$(P \to) \Rightarrow F \simeq F \circ (P +)$ writing $\Rightarrow$ for the exponentiation of functors and $(P\to) X = P \to X$ is a Napieran functor.
This can be shown using the Yoneda lemma. Then given a container 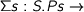$\Sigma s:S.P s \to$ and a functor 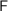we can reason as follows:

$\begin{eqnarray*} \lefteqn{ (\Sigma s:S.P s \to) \Rightarrow F }\\ & \simeq & \Pi s:S.(P s \to) \Rightarrow F \\ & \simeq & \Pi s:S.F \circ (+ P s) \end{eqnarray*}$

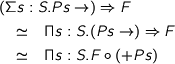
\begin{eqnarray*} \lefteqn{ (\Sigma s:S.P s \to) \Rightarrow F }\\ & \simeq & \Pi s:S.(P s \to) \Rightarrow F \\ & \simeq & \Pi s:S.F \circ (+ P s) \end{eqnarray*}

This shows that one can exponentiate any functor with a container (predicatively) and that exponent of containers is a container, since we know that 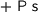+ P s is a container and containers are closed under composition and products. Expanding the definition gives rise to Paul’s definition.