Nottingham FP Lab Blog
Numbers vs Sets
by Thorsten on November 7, 2008.
Tagged as: Lunches.
To simplify: Mathematics has to do with numbers, while Computer Science is more concerned with types (let’s call them sets). On the level of the natural numbers there is a nice equivalence identfying a finite set with the number of its elements. The operations of addition and multiplication on numbers correspond to coproduct (or disjoint union) and (cartesian) product of sets. Indeed we even use the same symbols  and
and  . Exponentiation
. Exponentiation 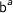 corresponds to function space
corresponds to function space  , indeed category theoreticians use the exponential notation for the latter.
, indeed category theoreticians use the exponential notation for the latter.
But then the ways part and the schism begins. For the Mathematicians the natural numbers are only half of the story (indeed a semiring) and they hasten to add the negative numbers. If we want to keep exponentiation, we can’t stop at the integers, we get the rational numbers 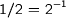 , algebraic reals
, algebraic reals  and even algebraic complex numbers
and even algebraic complex numbers  . The intuitive completion of these constructions are the complex numbers.
. The intuitive completion of these constructions are the complex numbers.
Negative sets don’t really make sense, we are more interested in infinite sets. E.g. we would like to have a fixpoint of successor: 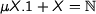 . Combining this with exponentiation leeds to larger sets like
. Combining this with exponentiation leeds to larger sets like  or ordinal notations
or ordinal notations
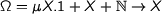 . This time the intuitive completion are sets.
. This time the intuitive completion are sets.
But the story may have a happy ending. Once we start to analyze operations on those spaces, a new analogy seems to emerge. E.g. differentiation is well known as an operation on complex functions, but as Conor McBride observed it also makes sense as an operation on functors, i.e. operations on sets. Not on all functors, but then differentiation doesn’t work on all functions either. The analogy carries further, and indeed we can use a variation of Taylor’s theorem to analyze datatypes. Hence, here we seem to have a new union, the glimpse of a generalized calculus applicable to operations in numbers and sets.
One of the areas where this analogy has been exploited is the theory of species, where ideas from calculus are exploited to prove theorems about the combinatorics of structures. To me much of the literature seems to be written from the perspective of Mathematicians who know numbers and try to use them to analyze sets. I’d prefer to do it the other way around, start with sets and see whether we can steal ideas from conventional calculus.
This is basically the introduction to a more technical talk about generalized species which I will post separately.
comments powered by Disqus